Gábor Domokos recently received the precious Gábor Dénes award. Interview at bme.hu (in Hungarian).
Gábor Dénes Award 2019
Ice eggs and ooids
Interesting natural phenomenon explained on index by our research group.

Figure: Ooid sand from The Bahamas.
Guest lecture: Bernd Krauskopf
Excitability and feedback: to pulse or not to pulse?
Bernd Krauskopf (University of Auckland)
joint work with Soizic Terrien and Neil Broderick (University of
Auckland), Anirudh Pammi and Sylvain Barbay (C2N, Paris-Saclay)
18 November, 2019
Department of Physics, 4pm
Abstract: Excitability is a very common phenomenon in the dynamics of many natural and engineered systems; examples are neurons, certain chemical reactions and laser systems. Being at equilibrium, an excitable system reacts to a sufficiently large perturbation by suddenly releasing a pulse of stored energy. Then the system needs some time to recover its level of stored energy. When excitable systems are coupling to themselves or to each other, they receive feedback with a delay time that is considerably larger than the pulse length. This may lead to very interesting pulsing dynamics. We demonstrate this here with an excitable micropillar laser with a feedback loop, or external cavity, generated by a regular mirror, which has been shown experimentally to be able to sustain trains of optical pulses. These can be triggered largely independently by optical perturbations injected into the laser, and they are then sustained simultaneously via feedback from the external cavity. A bifurcation analysis of a rate-equation model shows that the system has a number of periodic solutions with different numbers of equally spaced pulses as its only attractors. Hence, although coexisting pulse trains can seem independent on the timescale of the experiment, they correspond to very long transient dynamics. We determine the switching dynamics by studying the associated basins of attraction, which demonstrates that timing is everything when it comes to triggering or erasing pulse trains.

Guest lecture: Alain Goriely
On the shape of gravitating planets
Alain Goriely, University of Oxford
October 22, 2019
Abstract: A classic problem of elasticity is to determine the possible equilibria of a planet modelled as a homogeneous compressible spherical elastic body subject to its own gravitational field. In the absence of gravity the initial radius is given and the density is constant. With gravity and for small planets, the elastic deformations are small enough so that the spherical equilibria can be readily obtained by using the theory of linear elasticity. For larger or denser planets, large deformations are possible and surprising behaviours emerge as will be revealed during this talk.

The geometry of turbulence, Applied Mathematics Day 2019
Székelyhidi László (Universität Leipzig):
Rigid surfaces from Euclid to Nash and how to bend them.
October 16, 2019
16.30 BME K.150
“A compact surface is called rigid if the only length-preserving transformations of it are congruencies of the ambient space – in simple terms rigid surfaces are unbendable. Rigidity is a topic which is already found in Euclid’s Elements. Leonhard Euler conjectured in 1766 that every smooth compact surface is rigid. The young Augustin Cauchy found a proof in 1813 for convex polyhedra, but it took another 100 years until a proof for smooth convex surfaces appeared. Whilst it seems clear that convexity, and more generally curvature plays an important role for rigidity, it came as a shock to the world of geometry when John Nash showed in 1954 that every surface can be bent in an essentially arbitrary, albeit non-convex manner. The proof of Nash involves a highly intricate fractal-like construction, that has in recent years found applications in many different branches of applied mathematics, such as the theory of solid-solid phase transitions and hydrodynamical turbulence. The talk will provide an overview of this fascinating subject and present the most recent developments.”


(Source: http://hevea-project.fr/)
Uriel Frisch (CNRS, France):
Leonardo da Vinci, Tódor Kármán and many more: the decay of turbulence.
October 16, 2019
17.30 BME K.150
“Leonardo had a strong interest in mathematics (at the time, mostly geometry and simple algebraic equations). In the early part of his life, spent in Florence, Leonardo became interested in chaotic hydrodynamics (called by him, for the first time “turbulence”), a topic which will persist throughout his life. Examining the “turbulences” (eddies) in the river Arno he found in the late 1470 that the amplitude of the turbulence was decreasing very slowly in time, until it would come to rest (within the surrounding river). This topic would remain dormant for close to 5 centuries, until in 1938 Todor (Theodore) Karman, triggered by Geoffrey Taylor, established that the amplitude of the turbulence should decrease very slowly, indeed like an inverse power of the time elapsed. Three years later, Andrei Kolmogorov found an algebraic mistake in Karman’s calculation; Kolmogorov himself found another inverse power (5/7) of the time elapsed. This, likewise was wrong. In the talk we will present developments in a historical context and connect to recent progress on this topic. Very recently, we found that the law of decay of the amplitude need not be exactly an inverse of the time elapsed. Furthermore, more exotic laws of decay were obtained for “weak” (distributional) solutions using a Nash-like construction.”


BME- NEWS: „I started research with the support of an excellent group of professors”
Talk at the DDG2 conference
Mechanical complexity of complex polyhedra
Flórián Kovács, MTA-BME Morphodynamics Research Group
July 10, 2019
Discrete Geometry Days 2, Budapest
Abstract: Let P be a convex polyhedron with f faces, e edges and v vertices, and assume it is realized as a homogeneous solid having S stable, H saddle-type and U unstable equilibrium configurations (i.e., standing on a face, edge or vertex over a horizontal surface). Let mechanical complexity C(P) of P be defined as the difference between the sums f + e + v and S + H + U and define mechanical complexity C(S,U) of primary equilibrium classes (S,U)^E as the minimum of mechanical complexities of all polyhedra having S stable and U unstable equilibria. In this talk we show that mechanical complexity in any non-monostatic (i.e., S > 1 and U > 1) primary equilibrium class (S,U)^E equals the minimum of 2(f+v−S−U) over all polyhedra in the same class having simultaneously f faces and v vertices; thus, mechanical complexity of a class (S,U)^E is zero if and only if there exists P such that f = S and v = U. We also give both upper and lower bounds for C(S,U) in the cases S = 1 ≠ U and U = 1 ≠ S (a problem related to a question of Conway and Guy in 1969 asking about the minimal number of faces of convex polyhedra with only one stable equilibrium point), and we offer a complexity-dependent prize for C(1,1). Joint work with Gábor Domokos, Zsolt Lángi, Krisztina Regős and Péter T. Varga.
Guest lecturer: Boris A. Khesin
Integrability of pentagram maps and KdV hierarchies
Boris A. Khesin, University of Toronto
June 27, 2019
Abstract: We describe pentagram maps on polygons in any dimension, which extend R.Schwartz’s definition of the 2D pentagram map. Many of those maps turn out to be discrete integrable dynamical systems, while the corresponding continuous limits of such maps coincide with equations of the KdV hierarchy, generalizing the Boussinesq equation in 2D. We discuss their geometry, Lax forms, and interrelations between several recent pentagram generalizations.

National Scientific Conference Presentation Award 2019
Congratulations for Krisztina Regős on winning one of the four Presentation Awards on the National Scientific Student’s Conference 2019 with her presentation titled ‘Morphological analysis of fractured rock surfaces‘.
Applied Mathematics Day 2019.
Denis Weaire FRS (Trinity College, Dublin)
On growth and form (of bubbles)
29th April, 2019. 16:00
BME K150
“Bubbles and foams have always attracted the interest of artists, poets and philosophers (as well as small children). Physicists are similarly drawn to the subject, but with more precise aims – to understand the detailed structure of crowded bubbles and their competing growth, as well as their mechanical properties. Here we will concentrate mainly on structure, recalling the contributions of Plateau and Kelvin in the 19th century and their echoes down to the present time.”


Contributors: Douglas J. Jerolmack and Ferenc Kun
Douglas J. Jerolmack and Ferenc Kun attended our seminar on 13th April, 2019.


Insulin capsules inspired by the Gomboc
National Scientific Student’s Conference 2019
Results of the National Scientific Student’s Conference 2019:
Krisztina Regős Special prize
Péter Varga 2nd Prize
Congratulations to both of them!
Guest: Michel Potier-Ferry
Our guest Michel Potier-Ferry from University of Lorraine, France was a Reviewer and Member of the Doctoral committee at the PhD defense of Eszter Fehér.

PhD defense
Our member Eszter Fehér successfully defended her PhD thesis Wrinkling behavior of highly stretched thin films.
Brief summary: In the literature of the wrinkling of ultrathin films, theoretical models were often used to investigate phenomena that fall outside the range of validity of their assumptions. Contradictory results were published regarding the wrinkling of axially stretched, clamped, rectangular films. Based on the Föppl-von Kármán plate theory (FvK) wrin- kles appear on the surface and their amplitude scales with the macroscopic strain. A finite membrane strain extension of the FvK theory (eFvK) predicted that only a bounded region of the macroscopic strain and aspect ratio parameters exhibit wrinkling in the problem.
The first goal of the work is to verify these predictions experimentally. Secondly, the eFvK model was extended into directions, that are beneficial in the modeling of real-life structures. The effect of material and geometrical properties and nonlinearities on wrinkling was also examined in detail.
Orthotropy was incorporated into the model and its effect was investigated. By comparing the results of the orthotropic model and experiments carried out on pre- stressed polyurethane films, the predictions of the eFvK model were experimentally verified. Motivated by further experimental observations, a pseudoelastic model based on the Mullins effect was also proposed and it was shown, that it can explain the intriguing phenomenon arisen during the prestressing of polyurethane films.
The eFvK model was extended to curved surfaces, and it was shown, that the intrinsic curvature can reduce wrinkling. Finally, we carried out an investigation of the parameter space by letting the thickness of the film arbitrary small. We introduced the concept of disturbed zones near the clamps which gave a physical explanation of the aspect ratio dependency of the wrinkling in the model problem.In the literature of the wrinkling of ultrathin films, theoretical models were often used to investigate phenomena that fall outside the range of validity of their assumptions. Contradictory results were published regarding the wrinkling of axially stretched, clamped, rectangular films. Based on the Föppl-von Kármán plate theory (FvK) wrin- kles appear on the surface and their amplitude scales with the macroscopic strain. A finite membrane strain extension of the FvK theory (eFvK) predicted that only a bounded region of the macroscopic strain and aspect ratio parameters exhibit wrinkling in the problem.
The first goal of the work is to verify these predictions experimentally. Secondly, the eFvK model was extended into directions, that are beneficial in the modeling of real-life structures. The effect of material and geometrical properties and nonlineari- ties on wrinkling was also examined in detail.
Orthotropy was incorporated into the model and its effect was investigated. By comparing the results of the orthotropic model and experiments carried out on prestressed polyurethane films, the predictions of the eFvK model were experimentally verified. Motivated by further experimental observations, a pseudoelastic model based on the Mullins effect was also proposed and it was shown, that it can explain the intriguing phenomenon arisen during the prestressing of polyurethane films.
The eFvK model was extended to curved surfaces, and it was shown, that the intrinsic curvature can reduce wrinkling. Finally, we carried out an investigation of the parameter space by letting the thickness of the film arbitrary small. We introduced the concept of disturbed zones near the clamps which gave a physical explanation of the aspect ratio dependency of the wrinkling in the model problem.

Institutional Scientific Students’ Associations Conference 2018
At this year’s Institutional Scientific Students’ Associations Conference at the Budapest University of Technology and Economics, 3 presentations were related to Morphodynamics: Krisztina Regős (1st Prize + Pro Progressio Special Prize), Dániel Csallóközi (2nd Prize + Csonka Pál Special Prize), Péter Tamás Varga (3rd Prize).
Continue Reading “Institutional Scientific Students’ Associations Conference 2018”
Guest lecturer: Sir Michael Berry
Nature’s optics and our understanding of light
Sir Michael Berry
University of Bristol
December 12th, 2018 at 4 pm
BME, K134
Abstract: Optical phenomena visible to everyone abundantly illustrate important ideas in science and mathematics. The phenomena considered include rainbows, sparkling reflections on water, green flashes, earthlight on the moon, glories, daylight, crystals, and the squint moon. The concepts include refraction, wave interference, numerical experiments, asymptotics, Regge poles, polarization singularities, conical intersections, and visual illusions.

Guest lecturer: Bernd Krauskopf
Computing global invariant manifolds as a sequence of geodesic level sets
Bernd Krauskopf, University of Auckland
joint work with
Hinke Osinga, University of Auckland
May 16, 2018
Abstract: Steady-states and periodic orbits of saddle type of dynamical systems defined by ordinary differential equations come with stable and unstable manifolds. These invariant, global objects play a crucial role in organising the dynamics, for example, as basin boundaries and in the creation of chaotic attractors. We consider here global invariant manifolds of dimension two in three-dimensional systems. These are implicitely defined surfaces that can generally only be found by numerical means.
We present arguably the most geometric approach to finding and visualising these surfaces: we grow a manifold step by step from the steady-state of periodic orbit by computing a sequence of rings or bands at suitable geodesic distances. Our method is illustrated with several examples, including the Lorenz system.

Guest lecturer: Snorre H. Christiansen
Our guest lecturer Snorre H. Christiansen from University of Oslo gave us his talk on the 7th May 2018 with the title ‘Finite element complexes for the Stokes equation’.

Guest lecturer: Daniel Barreto
Our guest lecturer Daniel Barreto from Edinburgh Napier University gave us his talk on the 6th February 2018 with the title ‘Contact force entropy coordinates – Their relationship with critical states and shearing resistance’.

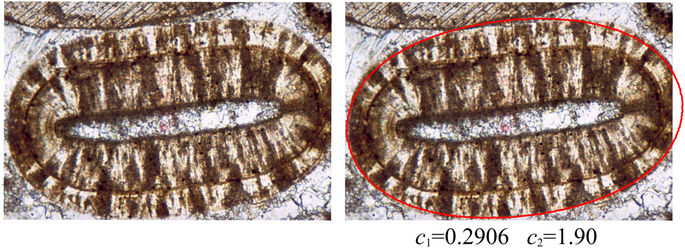
A new study on Ooid growth
Shape evolution of ooids: a geometric model
András A. Sipos, Gábor Domokos, Douglas J. Jerolmack
Abstract: Striking shapes in nature have been documented to result from chemical precipitation — such as terraced hot springs and stromatolites — which often proceeds via surface-normal growth. Another studied class of objects is those whose shape evolves by physical abrasion — the primary example being river and beach pebbles — which results in shape-dependent surface erosion. While shapes may evolve in a self-similar manner, in neither growth nor erosion can a surface remain invariant. Here we investigate a rare and beautiful geophysical problem that combines both of these processes; the shape evolution of carbonate particles known as ooids. We hypothesize that mineral precipitation, and erosion due to wave-current transport, compete to give rise to novel and invariant geometric forms. We show that a planar (2D) mathematical model built on this premise predicts time-invariant (equilibrium) shapes that result from a balance between precipitation and abrasion. These model results produce nontrivial shapes that are consistent with mature ooids found in nature.
New paper on ‘Oumuamua
The paper Explaining the Elongated Shape of ‘Oumuamua by the Eikonal Abrasion Mode (Gábor Domokos, András Á. Sipos, Gyula M. Szabó, Péter L. Várkonyi) was followed by increased media attention. It was mentioned on both national and international websites such as newsweek.com, bbc.com, hirado.hu.

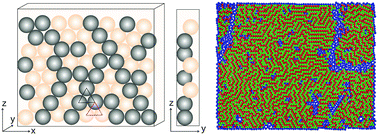
New paper on granular systems published
Frustrated packing in a granular system under geometrical confinement
Sára Lévay, David Fischer, Ralf Stannarius, Balázs Szabó, Tamás Börzsönyi and János Török
Abstract: Optimal packings of uniform spheres are solved problems in two and three dimensions. The main difference between them is that the two-dimensional ground state can be easily achieved by simple dynamical processes while in three dimensions, this is impossible due to the difference in the local and global optimal packings. In this paper we show experimentally and numerically that in 2 + ε dimensions, realized by a container which is in one dimension slightly wider than the spheres, the particles organize themselves in a triangular lattice, while touching either the front or rear side of the container. If these positions are denoted by up and down the packing problem can be mapped to a 1/2 spin system. At first it looks frustrated with spin-glass like configurations, but the system has a well defined ground state built up from isosceles triangles. When the system is agitated, it evolves very slowly towards the potential energy minimum through metastable states. We show that the dynamics is local and is driven by the optimization of the volumes of 7-particle configurations and by the vertical interaction between touching spheres.
Student Research Conference 2017
At this year’s Student Research Conference 4 presentations were related to Morphodynamics: Adria Kerekes & Dávid Büki (1st Prize), Dániel Csallóközi (2nd Prize), Julia Hegymegi (3rd Prize), Menyhért Gergye (3rd Prize + Best presentation award).
Continue Reading “Student Research Conference 2017”
Guest lecturer: Rocky Taylor
Morphodynamics of sea ice: exploring morphological evolution of ice rubble and ridges during the seasonal life cycle of deformed first-year sea ice
Rocky S. Taylor, Memorial University of Newfoundland, Canada
November 13, 2017
Abstract: Sea ice features in nature can take on many different forms. For marine and offshore engineering applications, ice loads during interactions with ice rubble and ice ridges are an important design consideration. Morphodynamic aspects of sea ice deformation and degradation processes are of interest in understanding the seasonal evolution of these features, since such methods may provide opportunities to simplify modelling of these highly complex processes. During deformation of a level ice sheet, it is of interest to understand how resultant distributions of block sizes and shapes are linked to the parent ice thickness and other environmental conditions. Similarly, for existing ice rubble and ridges, it is of interest how block shape evolution occurs during freezing/thawing cycles and how this influences the internal buoyancy forces on submerged ice blocks within a ridge. Such processes in turn influence rubble pile stability, since evolution of the shapes and associated centres of buoyancy for each block will change the distribution of stresses on the bonds between them. This can influence the degradation of strength of ice ridges, ultimately contributing to the breakdown of these features during spring thaw. These processes are of interest to help identify the key deterioration mechanisms for ridges, since it is not clear if this process would result in local progressive failure of a ridge (e.g. blocks shed away gradually from the outside with the failure front moving inward over time until the whole ridge is gone) or if there is sufficient reserve strength in the bonds so that the change in buoyancy results in a build-up of stresses due to these shifting buoyance forces that ultimately results in a sudden, global collapse of the whole ridge. Understanding these processes is important in developing new mathematical models, not only for modelling strength of deteriorated ridges during ice-structure interactions, but also for improving deterioration models that may be incorporated into larger-scale thermodynamic ice environmental models.

BRIEF BIOGRAPHY – ROCKY TAYLOR, PHD, P.ENG
Dr. Rocky Taylor is an Assistant Professor in Mechanical Engineering at Memorial University of Newfoundland in St. John’s, Canada, where he is also the Centre for Arctic Resource Development (CARD) Chair in Ice Mechanics. In this role he leads a team of researchers and graduate students working on Ice Compressive Failure Mechanics, Ice Rubble Mechanics, Ice Environmental Characterization and Ice-Structure Interaction Modelling. He has carried out field work in the Labrador Sea, Northern Newfoundland, the North Humberland Strait, the Caspian Sea, and the Barents Sea. He has more than 50 peer reviewed publications, has worked on many industry and academic projects and is currently a member of the ISO 19906 Canadian Review Committee.
New pre-print available
A shape evolution model under affine transformations
Gábor Domokos, Zsolt Lángi, Márk Mezei
Abstract: In this note we describe a discrete dynamical system acting on the similarity classes of a plane convex body within the affine class of the body. We find invariant elements in all affine classes, and describe the orbits of bodies in some special classes. We point out applications with abrasion processes of pebble shapes.
Guest lecturer: László Székelyhidi
Rigid surfaces and how Nash bent them
László Székelyhidi
Universität Leipzig
October 2, 2017
Abstract: A compact surface in R3 is called rigid if the only length-preserving transformations of it are congruencies of the ambient space – in simple terms rigid surfaces are unbendable. Rigidity is a topic which is already found in Euclid’s Elements. Euler conjectured in 1766 that every smooth compact surface is rigid. The young Cauchy found a proof in 1813 for convex polyhedra, but it took another 100 years until a proof for smooth convex surfaces appeared. Whilst it seems clear that convexity, and more generally curvature plays an important role for rigidity, it came as a shock to the world of geometry when J. Nash showed in 1954 that every surface can be bent in an essentially arbitrary, albeit non-convex manner. The proof of Nash involves a highly intricate fractal-like construction, that has in recent years found applications in many different branches of applied mathematics, such as elasticity and fluid mechanics. The talk will provide an overview of this fascinating subject and the most recent developments.

