A series of lectures on morphodynamics delivered at high schools in Hungary dates back to December, 2023: there are already ten different schools on the list. News and a video report are available about the lecture held on 14th March, 2025 in Kaposvár.
Gyula Farkas Memorial Award for Krisztina Regős
 The János Bolyai Mathematical Society decided on the Gyula Farkas Memorial Awards: one of the awardees in 2025 is Krisztina Regős, PhD student of the HUN-REN Morphodynamics Research Group.
The János Bolyai Mathematical Society decided on the Gyula Farkas Memorial Awards: one of the awardees in 2025 is Krisztina Regős, PhD student of the HUN-REN Morphodynamics Research Group.
Congratulations!
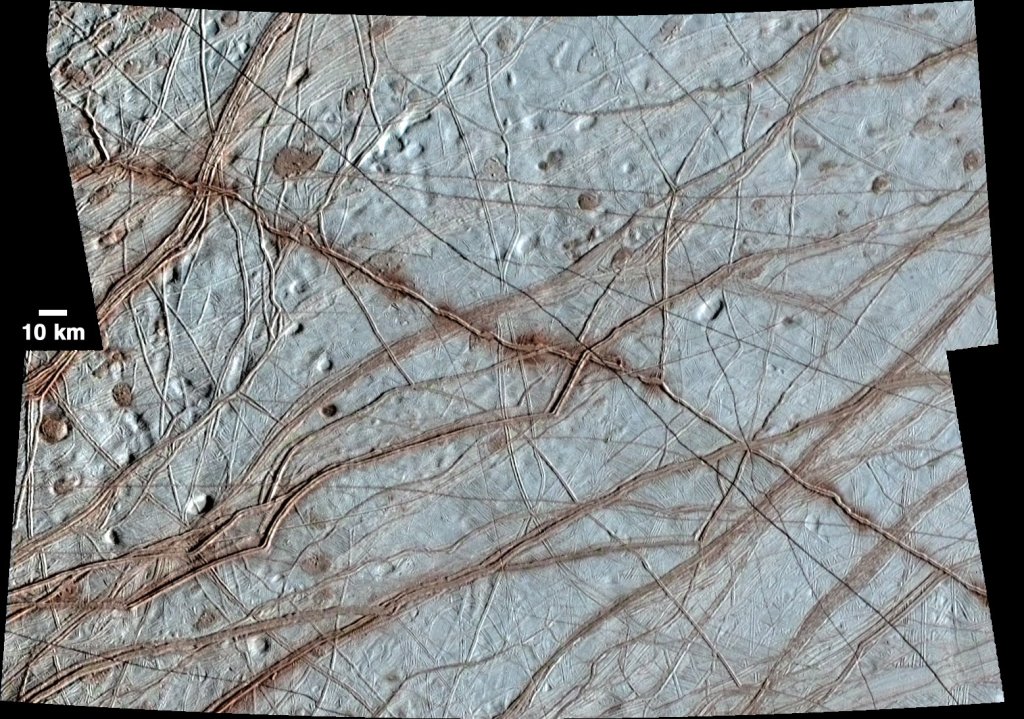
New paper and an interview on planetary surface mosaics
Decoding planetary surfaces by counting cracks
Sophie Silver, Douglas Jerolmack, Krisztina Regős, Gábor Domokos.
Abstract: Planets are often covered with thin cracked shells. From mud films to lithospheres of rock or ice, fracture networks form two-dimensional (2D) tessellations of convex polygons whose geometry encodes their genesis. Here, we chart the geometry of 2D fracture mosaics across the solar system, and decode their formative conditions using a new dynamical crack model. We show that mosaics can be projected onto a Symbolic Ternary Diagram, where the relative proportions of “T,” “X,” and “Y” junctions are uniquely related to contributions from distinct modes of fracture. Most planetary mosaics cluster in a region associated with hierarchical fracture networks, where sequential cracking favors formation of T junctions. Exceptions to this rule may betray the presence of water. Europa’s fracture networks stand apart due to the predominance of X junctions; this is a special feature of ice, where healing of cracks by refreezing of water allows new fractures to overprint older ones. Several fracture networks on Mars appear as outliers due to the high proportion of Y junctions. These patterns—previously interpreted as ancient mudcracks and frozen polar terrain, based on geological evidence—are consistent with the twisting of crack junctions by cyclic volume change. Our findings suggest that counting cracks could aid in the identification of other water-influenced planetary environments.
(See also the related interview at the website of BME.)
Field trip and international workshop in Spain
A group of researchers and students from the HUN-REN Morphodynamics Research Group made a visit to the Univerity of Vigo and Cedex, Madrid between 2-7 March. In addition to a field trip to rocking stones, the group participated in an international workshop on rock mechanics and geometry, hosted by the Cedex. 
New paper on a 2D collisional abrasion model
A Geometrically Motivated Two-Dimensional Collisional Abrasion Model to Resolve the Evolution of Natural Fragment Shapes
Balázs Havasi-Tóth, Eszter Fehér.
Abstract: In the present paper we propose a geometrically motivated mathematical model, which reveals the key features of natural coastal and fluvial fragment shape evolution from the earliest stages of the abrasion. Our collisional polygon model governs the evolution through an ordinary differential equation (ODE), which determines the rounding rate of initially sharp corners in the function of the size reduction of the fragment. As an approximation, the basic structure of our model adopts the concept of Bloore’s partial differential equation (PDE) in terms of the curvature-dependent local collisional frequency. We tested our model under various conditions and made comparisons with the predictions of Bloore’s PDE. Moreover, we applied the model to discover and quantify the mathematical conditions corresponding to typical and special shape evolution. By further extending our model to investigate the self-dual and mixed cases, we outline a possible explanation of the long-term preservation of initial pebble shape characteristics.

Institutional Scientific Students’ Associations Conference 2024
This year’s Institutional Scientific Students’ Associations Conference at the Budapest University of Technology and Economics was notably successful for the HUN-REN Research Group of Morphodynamics: four students of the group were among the winners of different prizes:
Continue Reading “Institutional Scientific Students’ Associations Conference 2024”
Lectures for high school students
A series of scientific informative lectures for interested high school students has been organized by the HUN-REN Morphodynamics Research Group.
- Kocsis Kinga: Ezer tonna márvány, avagy tér-idő utazás Michelangelo kőtömbjeihez (A thousand ton of marble or a time-space travel to the stones of Michelangelo)
- Szondi Máté: Alakevolúciós egyenlet használata membránfelületek számítására (Application of shape evolution equations for calculating membrane surfaces)
- Regős Krisztina: A diszkrét Gömböc nyomában (In the wake of a discrete Gömböc)
(Lovassy László High School, Veszprém, 8 December, 2023)
- Almádi Gergő: Tetraéderek egyensúlyairól (On equilibria of tetrahedra)
- Nagy Klaudia: Falak geometriája (The geometry of walls)
- Regős Krisztina: A diszkrét Gömböc nyomában (In the wake of a discrete Gömböc)
(Deák Ferenc High School, Budapest, 23 January, 2024) Link
- Regős Krisztina: A diszkrét Gömböc nyomában (In the wake of a discrete Gömböc)
- Ferencz Eszter: Repedéshálózatok időfejlődése, avagy a Gilbert-piaffe (Time evolution of crack networks or the Gilbert piaffe)
- Kocsis Kinga: Ezer tonna márvány, avagy tér-idő utazás Michelangelo kőtömbjeihez (A thousand ton of marble or a time-space travel to the stones of Michelangelo)
(Árpád High School, Budapest, 27 March, 2024)
- Almádi Gergő – Regős Krisztina: A diszkrét Gömböc nyomában (In the wake of a discrete Gömböc)
(Teleki Blanka High School, Budapest, 23 April, 2024)
- Domokos Gábor: A láthatatlan kocka (The invisible cube)
(Teleki Blanka High School, Székesfehérvár, 20 June, 2024)
- Domokos Gábor: Kemény sziklák és lágy cellák (Hard rocks and soft cells)
- Almádi Gergő: Repedéshálózatok időfejlődése, avagy a Gilbert-piaffe (Time evolution of crack networks or the Gilbert piaffe)
- Regős Krisztina: A diszkrét Gömböc nyomában (In the wake of a discrete Gömböc)
- Szondi Máté: Adhat-e ötletet a természetes kopás a héjszerkezetek tervzéséhez? (Can natural abrasion inspire the design of membrane structures?)
(Camp of Mathematics, organized by the Trefort Ágoston High School of Budapest, Visegrád, 19 October, 2024)
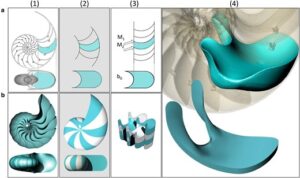
New paper on soft cells in geometry and biology
Soft cells and the geometry of seashells
Gábor Domokos, Alain Goriely, Ákos G. Horváth, Krisztina Regős.
Abstract: A central problem of geometry is the tiling of space with simple structures. The classical solutions, such as triangles, squares, and hexagons in the plane and cubes and other polyhedra in three-dimensional space are built with sharp corners and flat faces. However, many tilings in Nature are characterized by shapes with curved edges, nonflat faces, and few, if any, sharp corners. An important question is then to relate prototypical sharp tilings to softer natural shapes. Here, we solve this problem by introducing a new class of shapes, the soft cells, minimizing the number of sharp corners and filling space as soft tilings. We prove that an infinite class of polyhedral tilings can be smoothly deformed into soft tilings and we construct the soft versions of all Dirichlet–Voronoi cells associated with point lattices in two and three dimensions. Remarkably, these ideal soft shapes, born out of geometry, are found abundantly in nature, from cells to shells.
New flume in service at HUN-REN-BME Morphodynamics
 The inner width of the transparent cylinder of the flume is 10 cm, and the height is 25-50 cm. The desired speed of the circular flow can be set by pumping the water into the channel in a tangential direction from a tank in the bottom of the machine. It is expected that the device will be suitable for laboratory experiments
The inner width of the transparent cylinder of the flume is 10 cm, and the height is 25-50 cm. The desired speed of the circular flow can be set by pumping the water into the channel in a tangential direction from a tank in the bottom of the machine. It is expected that the device will be suitable for laboratory experiments  simulating the rather complicated behaviour of sediment particles in a river bed, thereby helping to gain a deeper understanding of the shape evolution of pebbles exposed to friction and collision.
simulating the rather complicated behaviour of sediment particles in a river bed, thereby helping to gain a deeper understanding of the shape evolution of pebbles exposed to friction and collision.
Successful PhD defense
Congratulations to Balázs Ludmány, who successfully defended his PhD thesis: An algorithmic approach to classical and mechanical shape descriptors of sedimentary particles (supervisor: Imre Szeberényi, Gábor Domokos).

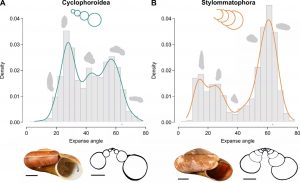
New paper on optimal shapes of snail shells
Many roads to success: alternative routes to building an economic shell in land snails
Barna Páll-Gergely, András Á. Sipos, Mathias Harzhauser, Aydın Örstan, Viola Winkler, Thomas A. Neubauer.
Abstract: Land snails exhibit an extraordinary variety of shell shapes. The way shells are constructed underlies biological and mechanical constraints that vary across gastropod clades. Here, we quantify shell geometry of the two largest groups, Stylommatophora and Cyclophoroidea, to assess the potential causes for variation in shell shape and its relative frequency. Based on micro-computed tomography scans, we estimate material efficiency through 2D and 3D generalizations of the isoperimetric ratio, quantifying the ratios between area and perimeter of whorl cross-sections (2D) and shell volume and surface (3D), respectively. We find that stylommatophorans optimize material usage through whorl overlap, which may have promoted the diversification of flat-shelled species. Cyclophoroids are bound to a circular cross-section because of their operculum; flat shells are comparatively rare. Both groups show similar solutions for tall shells, where local geometry has a smaller effect because of the double overlap between previous and current whorls. Our results suggest that material efficiency is a driving factor in the selection of shell geometry. Essentially, the evolutionary success of Stylommatophora likely roots in their higher flexibility to produce an economic shell.
Giovanni Barla Best Paper Award for Balázs Ludmány and coauthors
The paper A New Insight into the Stability of Precariously Balanced Rocks, authored by Balázs Ludmány, Gábor Domokos, András Sipos and others, was recognized by the Giovanni Barla Best Paper Award of 2023. The award is offered annually by the editors of Rock Mechanics and Rock Engineering to two or three papers published in the above journals. Congratulations!
Two lecturers in the top 100 of the BME
János Török and Krisztina Regős, members of our research group, are ranked 31st and 92th among all lecturers of the Budapest Univeristy of Technology and Economics.
Congratulations!
József Nádor Prize for Gergő Almádi
Gergő Almádi, student of the research group was awarded by József Nádor Prize on 12th March. The prize is traditionally given by the BME to students with outstanding candidature for the National Scholarship for Higher Education.
An interview with Krisztina Regős and Gergő Almádi at www.bme.hu
An interview with two young members of the HUN-REN Morphodynamics Research Group is published at www.bme.hu. Krisztina Regős and Gergő Almádi talk about the motivation of their research and experiences in publication.
A chapter in Hungarian Space Caleidoscope 2023/24
A chapter is dedicated to the HUN-REN Morphodynamics Research group in Hungarian Space Caleidoscope 2023/24. It is related to the research on the elongated shape of Oumuamua.
Public lecture of Sándor Bozóki on monostable convex polyhedra
A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by Sándor Bozóki. The lecture (in Hungarian) is available at the following link:
Proof of non-existence of mono-unstable polyhedra by means of inequalities (Monoinstabil poliéderek nemlétezésének igazolása egyenlőtlenségekkel)
Institutional Scientific Students’ Associations Conference 2023
At this year’s Institutional Scientific Students’ Associations Conference at the Budapest University of Technology and Economics, five presentations were related to Morphodynamics: Máté Szondi (1st Prize + Pro Progressio Special Prize), Gergő Almádi (1st Prize), Gergő Almádi and Eszter Ferencz (3rd Prize), Kinga Kocsis (Special award of the Department of Geometry and Morphology + Special award for presentation), Emese Sarolta Encz and Gergely Barta (Special award of the Department of Geometry and Morphology).
Continue Reading “Institutional Scientific Students’ Associations Conference 2023”
Public lecture of András Sipos on shape evolution in Nature
 A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by András Sipos. The lecture (in Hungarian) is available at the following link:
A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by András Sipos. The lecture (in Hungarian) is available at the following link:
Geometry and evolution of shapes in Nature (Geometria és alakfejlődés a természetben)
Applied Mathematics Day 2023
Two lectures will be presented at BME Applied Mathematics Day 2023, organized on 5th December, BME building Q, auditorium AF14.

A portrait of Gábor Domokos in MIT Technology Review
 A professional portrait of Gábor Domokos, leader of the HUN-REN-BME Morphodynamics Researh Group, has recently been published in MIT Technology Review by Elise Cutts.
A professional portrait of Gábor Domokos, leader of the HUN-REN-BME Morphodynamics Researh Group, has recently been published in MIT Technology Review by Elise Cutts.
New paper about the equilibria of tetrahedra
On Equilibria of Tetrahedra
Gergő Almádi, Robert J. MacG. Dawson, Gábor Domokos, and Krisztina Regős.
The paper focuses on the number of stable and unstable equilibria of tetrahedra with different mass distributions. The authors show that monostable tetrahedra exists with a suitably chosen distribution of density and, if a tetrahedron is monostable on one face, it can be made monostable on any other face with another distribution of density. Beyond tetrahedra, a construction for mono-monostatic pentahedra is also given in the paper.
Sándor Bozóki nominated full professor
 Sándor Bozóki, member of the HUN-REN Morphodynamics Research Group has been nominated full professor by the President of Republic on 5th September. Congratulations!
Sándor Bozóki, member of the HUN-REN Morphodynamics Research Group has been nominated full professor by the President of Republic on 5th September. Congratulations!
New paper on a 21-vertex mono-monostatic object with point masses
Conway’s Spiral and a Discrete Gömböc with 21 Point Masses
Gábor Domokos, Flórián Kovács.
Abstract: We show an explicit construction in three dimensions for a convex, mono-monostatic polyhedron (i.e., having exactly one stable and one unstable equilibrium) with 21 vertices and 21 faces. This polyhedron is a 0-skeleton, with equal masses located at each vertex. The above construction serves as an upper bound for the minimal number of faces and vertices of mono-monostatic 0-skeletons and complements the recently provided lower bound of 8 vertices. This is the first known construction of a mono-monostatic polyhedral solid. We also show that a similar construction for homogeneous distribution of mass cannot result in a mono-monostatic solid.
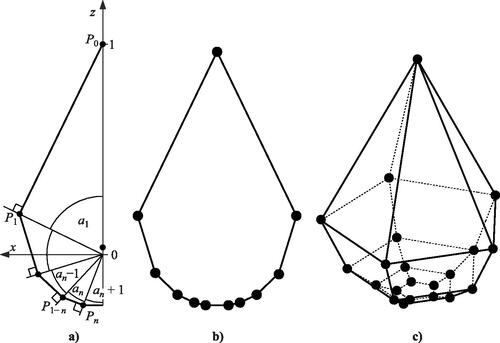
New paper on a possible evolution model of crack networks and other natural patterns
An Evolution Model for Polygonal Tessellations as Models for Crack Networks and Other Natural Patterns
Péter Bálint, Gábor Domokos, Krisztina Regős.
Abstract: We introduce and study a general framework for modeling the evolution of crack networks. The evolution steps are triggered by exponential clocks corresponding to local micro-events, and thus reflect the state of the pattern. In an appropriate simultaneous limit of pattern domain tending to infinity and time step tending to zero, a continuous time model, specifically a system of ODE is derived that describes the dynamics of averaged quantities. In comparison with the previous, discrete time model, studied recently by two of the present three authors, this approach has several advantages. In particular, the emergence of non-physical solutions characteristic to the discrete time model is ruled out in the relevant nonlinear version of the new model. We also comment on the possibilities of studying further types of pattern formation phenomena based on the introduced general framework.
Rocking stones in Tasmania
 ENSHRINE is a group of volunteer researchers, dedicated to preserve the natural heritage of Tasmania, Australia. Their studies on the behaviour of rocking stones, found in a large number in the area, were also based on some results of the MTA-BME Research Group for Morphodynamics (https://listthemountain.org/natural-features/rocking-stone).
ENSHRINE is a group of volunteer researchers, dedicated to preserve the natural heritage of Tasmania, Australia. Their studies on the behaviour of rocking stones, found in a large number in the area, were also based on some results of the MTA-BME Research Group for Morphodynamics (https://listthemountain.org/natural-features/rocking-stone).
Krisztina Regős in the “top 30 under 30” by Forbes.hu
Krisztina Regős, PhD student of the Morphodynamics Research Group was mentioned among the top 30 of most successful people under 30 in Hungary by Forbes.
Congratulations!
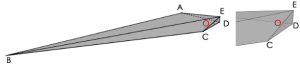
New paper on the smallest mono-unstable convex polyhedron with point masses
The smallest mono-unstable convex polyhedron with point masses has 8 faces and 11 vertices
Dávid Papp, Krisztina Regős, Gábor Domokos, Sándor Bozóki
Abstract: In the study of monostatic polyhedra, initiated by John H. Conway in 1966, the main question is to construct such an object with the minimal number of faces and vertices. By distinguishing between various material distributions and stability types, this expands into a small family of related questions. While many upper and lower bounds on the necessary numbers of faces and vertices have been established, none of these questions has been so far resolved. Adapting an algorithm presented in Bozóki et al. (2022), here we offer the first complete answer to a question from this family: by using the toolbox of semidefinite optimization to efficiently generate the hundreds of thousands of infeasibility certificates, we provide the first-ever proof for the existence of a monostatic polyhedron with point masses, having minimal number (V=11) of vertices (Theorem 3) and a minimal number (F=8) of faces. We also show that V=11 is the smallest number of vertices that a mono-unstable polyhedron can have in all dimensions greater than 1.
The World’s largest Gömböc on display in Paris
The “Gömböc” is on permanent display since 17th April, 2023 at Pompidou Centre, Paris. The largest copy of Gömböc ever made of a single piece of material was introduced in the presence of one of its inventors, Gábor Domokos.
National Scientific Students’ Associations Conference 2023
Several presentations were held in the session for Mathematics, Physics and Geosciences of the 36th National Scientific Students’ Associations Conference in relation with the Morphodynamics Research Group. Gergő Almádi has been awarded by 3rd prize for his presentation entitled Inhomogén politópok mechanikai komplexitása – avagy van-e egy tetraédernek lelke?, under the supervision of Gábor Domokos and Krisztina Regős. Ágoston Szesztay (Iteratív módon csonkolt poliéderek statikai egyenúlyáról) and Máté Szondi (A kvantummechanikai állapottér egy felbontása által indukált geometria) got special prizes.
Continue Reading “National Scientific Students’ Associations Conference 2023”
New paper on polygonal tessellations in nanochemistry
Polygonal tessellations as predictive models of molecular monolayers
Krisztina Regős et al.
Abstract: Molecular self-assembly plays a very important role in various aspects of technology as well as in biological systems. Governed by covalent, hydrogen or van der Waals interactions–self-assembly of alike molecules results in a large variety of complex patterns even in two dimensions (2D). Prediction of pattern formation for 2D molecular networks is extremely important, though very challenging, and so far, relied on computationally involved approaches such as density functional theory, classical molecular dynamics, Monte Carlo, or machine learning. Such methods, however, do not guarantee that all possible patterns will be considered and often rely on intuition. Here, we introduce a much simpler, though rigorous, hierarchical geometric model founded on the mean-field theory of 2D polygonal tessellations to predict extended network patterns based on molecular-level information. Based on graph theory, this approach yields pattern classification and pattern prediction within well-defined ranges. When applied to existing experimental data, our model provides a different view of self-assembled molecular patterns, leading to interesting predictions on admissible patterns and potential additional phases. While developed for hydrogen-bonded systems, an extension to covalently bonded graphene-derived materials or 3D structures such as fullerenes is possible, significantly opening the range of potential future applications.

New paper on precariously balanced rocks
A New Insight into the Stability of Precariously Balanced Rocks
Balázs Ludmány, Ignacio Pérez-Rey, Gábor Domokos, Mauro Muñiz-Menéndez, Leandro R. Alejano, András Á. Sipos
Abstract: Recently it became increasingly evident that the statistical distributions of size and shape descriptors of sedimentary particles reveal crucial information on their evolution and may even carry the fingerprints of their provenance as fragments. However, to unlock this trove of information, measurement of traditional geophysical shape descriptors (mostly detectable on 2D projections) is not sufficient; fully spherical 3D imaging and mathematical algorithms suitable to extract new types of inherently 3D shape descriptors are necessary. Available 3D imaging technologies force users to choose either speed or full sphericity. Only partial morphological information can be extracted in the absence of the latter (e.g., LIDAR imaging). In the case of fully spherical imaging, speed was proved to be prohibitive for obtaining meaningful statistical samples, and inherently 3D shape descriptors were not extracted. Here we present a new method by complementing a commercial, portable 3D scanner with simple hardware to quickly obtain fully spherical 3D datasets from large collections of sedimentary particles. We also present software for the automated extraction of 3D shapes and automated measurement of inherently 3D-shape properties. This technique allows for examining large samples without the need for transportation or storage of the samples, and it may also facilitate the collaboration of geographically distant research groups. We validated our software on a large sample of pebbles by comparing previously hand-measured parameters with the results of automated shape analysis. We also tested our hardware and software tools on a large pebble sample in Kawakawa Bay, New Zealand.

New paper on 3D pebble scanning
Fully spherical 3D datasets on sedimentary particles: Fast measurement and evaluation
Eszter Fehér, Balázs Havasi-Tóth, Balázs Ludmány
Abstract: Recently it became increasingly evident that the statistical distributions of size and shape descriptors of sedimentary particles reveal crucial information on their evolution and may even carry the fingerprints of their provenance as fragments. However, to unlock this trove of information, measurement of traditional geophysical shape descriptors (mostly detectable on 2D projections) is not sufficient; fully spherical 3D imaging and mathematical algorithms suitable to extract new types of inherently 3D shape descriptors are necessary. Available 3D imaging technologies force users to choose either speed or full sphericity. Only partial morphological information can be extracted in the absence of the latter (e.g., LIDAR imaging). In the case of fully spherical imaging, speed was proved to be prohibitive for obtaining meaningful statistical samples, and inherently 3D shape descriptors were not extracted. Here we present a new method by complementing a commercial, portable 3D scanner with simple hardware to quickly obtain fully spherical 3D datasets from large collections of sedimentary particles. We also present software for the automated extraction of 3D shapes and automated measurement of inherently 3D-shape properties. This technique allows for examining large samples without the need for transportation or storage of the samples, and it may also facilitate the collaboration of geographically distant research groups. We validated our software on a large sample of pebbles by comparing previously hand-measured parameters with the results of automated shape analysis. We also tested our hardware and software tools on a large pebble sample in Kawakawa Bay, New Zealand.
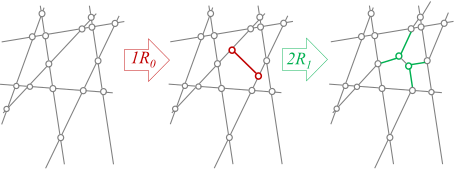
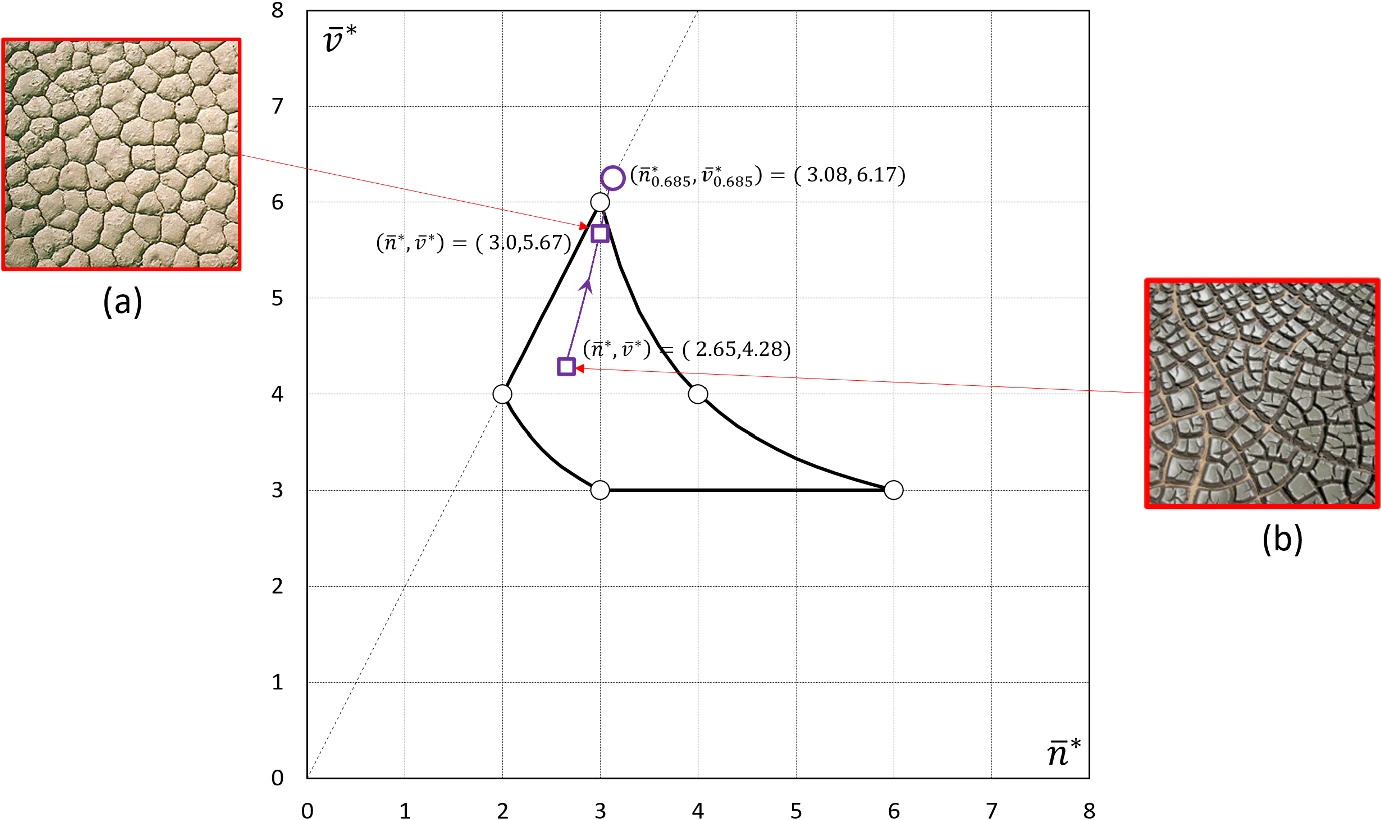
New paper on the evolution of fracture networks
A discrete time evolution model for fracture networks
Gábor Domokos, Krisztina Regős
Abstract: We examine geological crack patterns using the mean field theory of convex mosaics. We assign the pair (n̅∗, v̅∗) of average corner degrees to each crack pattern and we define two local, random evolutionary steps R0 and R1, corresponding to secondary fracture and rearrangement of cracks, respectively. Random sequences of these steps result in trajectories on the (n̅∗, v̅∗) plane. We prove the existence of limit points for several types of trajectories. Also, we prove that cell density ρ̅=n̅∗/v̅∗ increases monotonically under any admissible trajectory.
New paper on k-diametral point configurations
On k-diametral point configurations in Minkowski spaces
Károly Bezdek, Zsolt Lángi
Abstract: The structure of k-diametral point configurations in Minkowski d-space is shown to be closely related to the properties of k-antipodal point configurations in ℝd. In particular, the maximum size of k-diametral point configurations of Minkowski d-spaces is obtained for given k≥2 and d≥2 generalizing Petty’s results on equilateral sets in Minkowski spaces. Furthermore, bounds are derived for the maximum size of k-diametral point configurations in given Minkowski d-space (resp., Euclidean d-space). Some of these results have analogues for point sets, which are discussed as well. In the proofs convexity methods are combined with volumetric estimates and combinatorial properties of diameter graphs.
Interview with Gábor Domokos at perpal.hu
An interview with Gábor Domokos, one of the discoverers of Gömböc has recently been published at perpal.hu.
Beyond the history of Gömböc, the talk highlights the mutual impact the discovery and scientific thinking may have on each other.
Recognition of Zsolt Lángi at the Celebration of Hungarian Science
At the ceremony on 21 November, organized as part of the Celebration of Hungarian Science program series, Zsolt Lángi was also given a recognition by the Rector of University for having received the “Bolyai plakett” this year.
Congratulations!
Institutional Scientific Students’ Associations Conference 2022
At this year’s Institutional Scientific Students’ Associations Conference at the Budapest University of Technology and Economics, 4 presentations were related to Morphodynamics: Gergő Almádi (1st Prize + Pro Progressio Special Prize), Ágoston Szesztay (1st Prize), Klaudia Nagy (Csonka Pál Special Prize), Balázs Sárossi (2nd Prize).
Continue Reading “Institutional Scientific Students’ Associations Conference 2022”
Abrasion experiments at Centre de Recherches Pétrographiques et Géochimiques, Nancy
 This October, Eszter Fehér and Balázs Havasi-Tóth visited Jérôme Lavé in the Centre de Recherches Pétrographiques et Géochimiques, Nancy to carry out abrasion experiments on concrete and sandstone cubes in a Flume. The concrete cubes were identified by RFID tags. During the experiments, the geometry of the abraded cubes was 3D scanned and their evolution was compared to theoretical predictions of abrasion models. It was also investigated how the movement of the pebbles depend on the pebble shape in the artificial river conditions of a Flume.
This October, Eszter Fehér and Balázs Havasi-Tóth visited Jérôme Lavé in the Centre de Recherches Pétrographiques et Géochimiques, Nancy to carry out abrasion experiments on concrete and sandstone cubes in a Flume. The concrete cubes were identified by RFID tags. During the experiments, the geometry of the abraded cubes was 3D scanned and their evolution was compared to theoretical predictions of abrasion models. It was also investigated how the movement of the pebbles depend on the pebble shape in the artificial river conditions of a Flume.
The concrete cubes were designed and created by Károly Péter Juhász, JKP Static. Here is a video of the concreting and the installation of RFID tags:
Lecture at the Stuart Weitzman School of Design
Gábor Domokos will give a lecture “The invisible cube” at the University of Pennsylvania Stuart Weitzman School of Design on 16th February, at 6pm (Central European Time). The lecture gives insight into the work of the Morphology and Applied Geometry Department and the Morphodynamics research group. Follow the lecture online: zoom link.

Successful PhD defense
Congratulations to Sára Lévay, who successfully defended her PhD thesis: Self-organizing processes in granular materials (supervisor: János Török).

Another paper in Aequationes Mathematicae
An analogue of a theorem of Steinitz for ball polyhedra in R-3
Sami Mezal Almohammad, Zsolt Lángi, Márton Naszódi
Abstract: Steinitz’s theorem states that a graph G is the edge-graph of a 3-dimensional convex polyhedron if and only if, G is simple, plane and 3-connected. We prove an analogue of this theorem for ball polyhedra, that is, for intersections of finitely many unit balls in ℝ3.
Scanning pebbles in Siena
After our short visit and consultation in Sienna, Italy, before the global pandemic breakout, our colleagues finally had the opportunity to construct their own scanning equipment. We are looking forward to see their scanning results and experiences with the newly built devices.


Gomboc software in sailing
The Gomboc simulation software – whose name was chosen after the Gömböc of Gábor Domokos and Péter Várkonyi – played a crucial role in the the 36th America’s cup.
Read more (in Hungarian): A MAGYAR GÖMBÖCRŐL ELNEVEZETT GOMBOC SZOFTVERREL DIADALMASKODOTT A GYŐZTES CSAPAT A VILÁG LEGELITEBB VITORLÁSVERSENYÉN
An article about the Gomboc software in the 35th America’s cup (in English): Gomboc: A design high-flier for ETNZ
PhD defense
Our member Eszter Fehér successfully defended her PhD thesis Wrinkling behavior of highly stretched thin films.
Brief summary: In the literature of the wrinkling of ultrathin films, theoretical models were often used to investigate phenomena that fall outside the range of validity of their assumptions. Contradictory results were published regarding the wrinkling of axially stretched, clamped, rectangular films. Based on the Föppl-von Kármán plate theory (FvK) wrin- kles appear on the surface and their amplitude scales with the macroscopic strain. A finite membrane strain extension of the FvK theory (eFvK) predicted that only a bounded region of the macroscopic strain and aspect ratio parameters exhibit wrinkling in the problem.
The first goal of the work is to verify these predictions experimentally. Secondly, the eFvK model was extended into directions, that are beneficial in the modeling of real-life structures. The effect of material and geometrical properties and nonlinearities on wrinkling was also examined in detail.
Orthotropy was incorporated into the model and its effect was investigated. By comparing the results of the orthotropic model and experiments carried out on pre- stressed polyurethane films, the predictions of the eFvK model were experimentally verified. Motivated by further experimental observations, a pseudoelastic model based on the Mullins effect was also proposed and it was shown, that it can explain the intriguing phenomenon arisen during the prestressing of polyurethane films.
The eFvK model was extended to curved surfaces, and it was shown, that the intrinsic curvature can reduce wrinkling. Finally, we carried out an investigation of the parameter space by letting the thickness of the film arbitrary small. We introduced the concept of disturbed zones near the clamps which gave a physical explanation of the aspect ratio dependency of the wrinkling in the model problem.In the literature of the wrinkling of ultrathin films, theoretical models were often used to investigate phenomena that fall outside the range of validity of their assumptions. Contradictory results were published regarding the wrinkling of axially stretched, clamped, rectangular films. Based on the Föppl-von Kármán plate theory (FvK) wrin- kles appear on the surface and their amplitude scales with the macroscopic strain. A finite membrane strain extension of the FvK theory (eFvK) predicted that only a bounded region of the macroscopic strain and aspect ratio parameters exhibit wrinkling in the problem.
The first goal of the work is to verify these predictions experimentally. Secondly, the eFvK model was extended into directions, that are beneficial in the modeling of real-life structures. The effect of material and geometrical properties and nonlineari- ties on wrinkling was also examined in detail.
Orthotropy was incorporated into the model and its effect was investigated. By comparing the results of the orthotropic model and experiments carried out on prestressed polyurethane films, the predictions of the eFvK model were experimentally verified. Motivated by further experimental observations, a pseudoelastic model based on the Mullins effect was also proposed and it was shown, that it can explain the intriguing phenomenon arisen during the prestressing of polyurethane films.
The eFvK model was extended to curved surfaces, and it was shown, that the intrinsic curvature can reduce wrinkling. Finally, we carried out an investigation of the parameter space by letting the thickness of the film arbitrary small. We introduced the concept of disturbed zones near the clamps which gave a physical explanation of the aspect ratio dependency of the wrinkling in the model problem.


