An interview with Gábor Domokos, leader of the HUN-REN Morphodynamics research group appeared in HVG. The discussion addresses, among others, new achievements of the group as soft cell and mono-monostatic tetrahedron named “Bille”, possibilities and difficulties of young researchers, cooperation with NASA and questions that will probably not be answered even by AI.
The story of Bille, the mono-monostatic tetrahedron
As a proof for a 40-year-old conjecture, Gábor Domokos and Gergő Almádi, members of our research group proved the existence of a mono-monostatic tetrahedron in a joint research with Robert Dawson, St. Mary’s University. Even in 1984, J. H. Conway conjectured that there might exist inhomogeneous tetrahedra with only one stable equilibrium. The present research proved that such tetrahedron with only one stable and one unstable equilibrium exists as well.

To illustrate the strange behaviour, a prototype named “Bille” is also presented to the public. Further details are provided by the Quanta magazine.
New paper and an interview on planetary surface mosaics
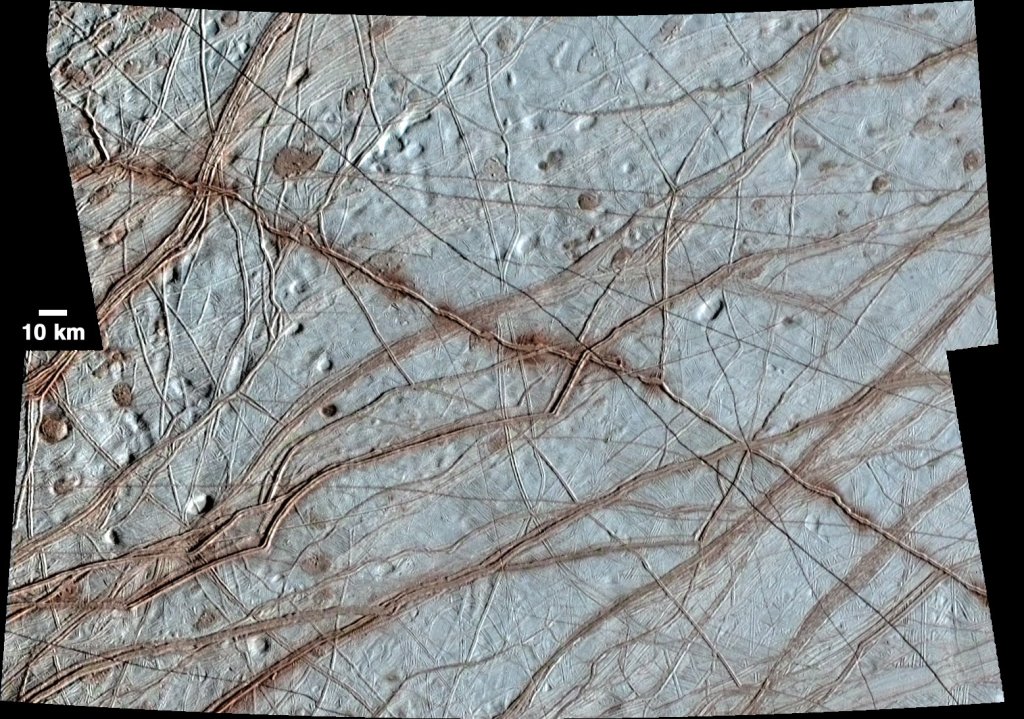
Decoding planetary surfaces by counting cracks
Sophie Silver, Douglas Jerolmack, Krisztina Regős, Gábor Domokos.
Abstract: Planets are often covered with thin cracked shells. From mud films to lithospheres of rock or ice, fracture networks form two-dimensional (2D) tessellations of convex polygons whose geometry encodes their genesis. Here, we chart the geometry of 2D fracture mosaics across the solar system, and decode their formative conditions using a new dynamical crack model. We show that mosaics can be projected onto a Symbolic Ternary Diagram, where the relative proportions of “T,” “X,” and “Y” junctions are uniquely related to contributions from distinct modes of fracture. Most planetary mosaics cluster in a region associated with hierarchical fracture networks, where sequential cracking favors formation of T junctions. Exceptions to this rule may betray the presence of water. Europa’s fracture networks stand apart due to the predominance of X junctions; this is a special feature of ice, where healing of cracks by refreezing of water allows new fractures to overprint older ones. Several fracture networks on Mars appear as outliers due to the high proportion of Y junctions. These patterns—previously interpreted as ancient mudcracks and frozen polar terrain, based on geological evidence—are consistent with the twisting of crack junctions by cyclic volume change. Our findings suggest that counting cracks could aid in the identification of other water-influenced planetary environments.
(See also the related interview at the website of BME.)
Public lecture of Sándor Bozóki on monostable convex polyhedra
A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by Sándor Bozóki. The lecture (in Hungarian) is available at the following link:
Proof of non-existence of mono-unstable polyhedra by means of inequalities (Monoinstabil poliéderek nemlétezésének igazolása egyenlőtlenségekkel)
Public lecture of András Sipos on shape evolution in Nature
 A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by András Sipos. The lecture (in Hungarian) is available at the following link:
A public lecture has been presented within the framework of Celebration of Hungarian Science (“Magyar tudomány ünnepe”) by András Sipos. The lecture (in Hungarian) is available at the following link:
Geometry and evolution of shapes in Nature (Geometria és alakfejlődés a természetben)
Krisztina Regős in the “top 30 under 30” by Forbes.hu
Krisztina Regős, PhD student of the Morphodynamics Research Group was mentioned among the top 30 of most successful people under 30 in Hungary by Forbes.
Congratulations!
The World’s largest Gömböc on display in Paris
The “Gömböc” is on permanent display since 17th April, 2023 at Pompidou Centre, Paris. The largest copy of Gömböc ever made of a single piece of material was introduced in the presence of one of its inventors, Gábor Domokos.
Interview with Krisztina Regős at forbes.hu
An interview with Krisztina Regős, graduate student of the Faculty of Architecture of BME and her supervisor, Gábor Domokos has recently been published at forbes.hu.
The conversation reveals how Gömböc inspires young researchers, specifically how this discovery influenced Krisztina’s further research.
Gomboc software in sailing
The Gomboc simulation software – whose name was chosen after the Gömböc of Gábor Domokos and Péter Várkonyi – played a crucial role in the the 36th America’s cup.
Read more (in Hungarian): A MAGYAR GÖMBÖCRŐL ELNEVEZETT GOMBOC SZOFTVERREL DIADALMASKODOTT A GYŐZTES CSAPAT A VILÁG LEGELITEBB VITORLÁSVERSENYÉN
An article about the Gomboc software in the 35th America’s cup (in English): Gomboc: A design high-flier for ETNZ
Science Magazine top 10
Science Magazine included the paper “Plato’s cube and the natural geometry of fragmentation” in the top 10 non-covid science news stories of 2020.
List of the top 10 science news stories of 2020:
Top news stories of 2020
Podcast episode:
Breakthrough of the Year, top online news, and science book highlights (9:36 – 12:40)
Quanta Magazine article
An outstanding article from Joshua Sokol Scientists Uncover the Universal Geometry of Geology about the paper “Plato’s cube and the natural geometry of fragmentation” in Quanta Magazine.
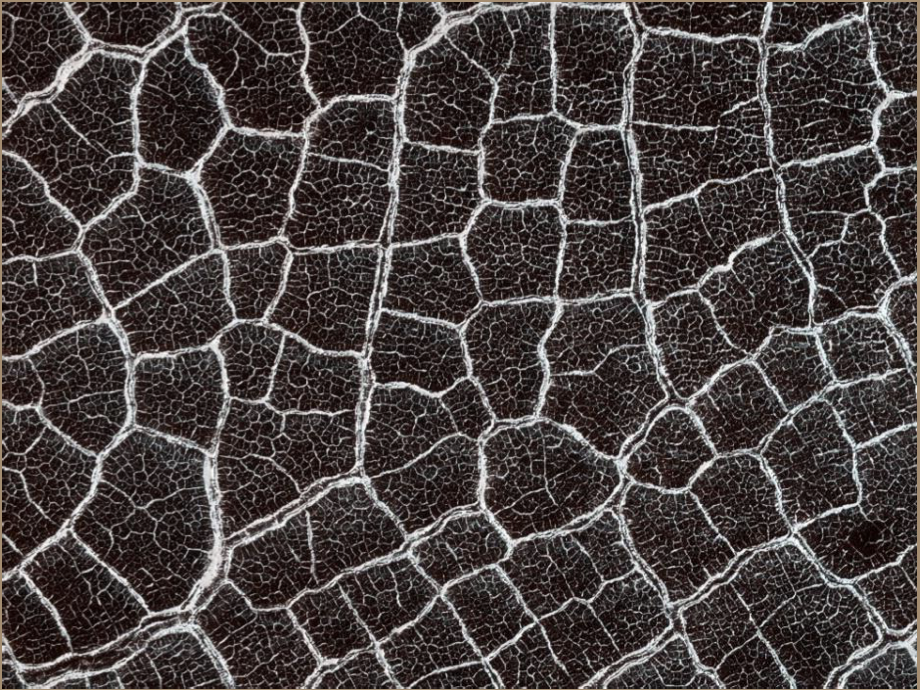
New paper on fragmentation
Plato’s cube and the natural geometry of fragmentation
G. Domokos, D.J. Jerolmack, F. Kun, J. Török
arxiv:1912.04628
Abstract: Plato envisioned Earth’s building blocks as cubes, a shape rarely found in nature. The solar system is littered, however, with distorted polyhedra—shards of rock and ice produced by ubiquitous fragmentation. We apply the theory of convex mosaics to show that the average geometry of natural two-dimensional (2D) fragments, from mud cracks to Earth’s tectonic plates, has two attractors: “Platonic” quadrangles and “Voronoi” hexagons. In three dimensions (3D), the Platonic attractor is dominant: Remarkably, the average shape of natural rock fragments is cuboid. When viewed through the lens of convex mosaics, natural fragments are indeed geometric shadows of Plato’s forms. Simulations show that generic binary breakup drives all mosaics toward the Platonic attractor, explaining the ubiquity of cuboid averages. Deviations from binary fracture produce more exotic patterns that are genetically linked to the formative stress field. We compute the universal pattern generator establishing this link, for 2D and 3D fragmentation.
The article was followed by increased media attention. Here is a list of the international and national mentions of the MTA-BME Morphodynamics Research Group: Media mentions.
Ice eggs and ooids
Interesting natural phenomenon explained on index by our research group.

Figure: Ooid sand from The Bahamas.
Insulin capsules inspired by the Gomboc
New paper on ‘Oumuamua
The paper Explaining the Elongated Shape of ‘Oumuamua by the Eikonal Abrasion Mode (Gábor Domokos, András Á. Sipos, Gyula M. Szabó, Péter L. Várkonyi) was followed by increased media attention. It was mentioned on both national and international websites such as newsweek.com, bbc.com, hirado.hu.
