A discrete time evolution model for fracture networks
Gábor Domokos, Krisztina Regős
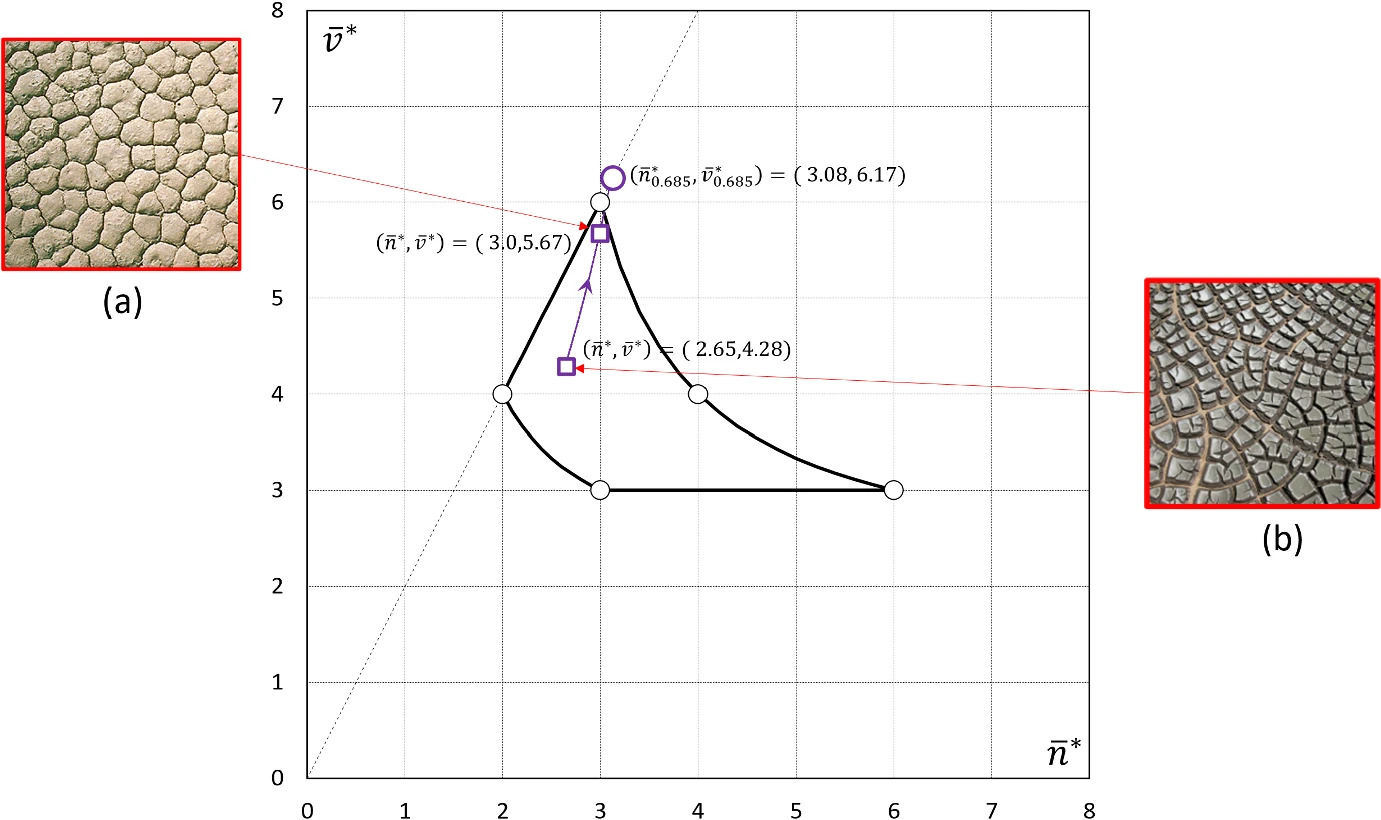
Abstract: We examine geological crack patterns using the mean field theory of convex mosaics. We assign the pair (n̅∗, v̅∗) of average corner degrees to each crack pattern and we define two local, random evolutionary steps R0 and R1, corresponding to secondary fracture and rearrangement of cracks, respectively. Random sequences of these steps result in trajectories on the (n̅∗, v̅∗) plane. We prove the existence of limit points for several types of trajectories. Also, we prove that cell density ρ̅=n̅∗/v̅∗ increases monotonically under any admissible trajectory.