The Morphodynamics Group had a session titled ‘Geometry’ in the 2021 TDK Conference. Five students participated in the session and received numerous awards. Congratulations!
Krisztina Regős (1st Prize + Rector’s Award), Anna Viczián (1st Prize), Ágoston Szesztay (3rd Prize + Csonka Pál Special Prize), Klaudia Nagy (Department’s Special Prize), Máté Szondi (Metszet Journal Special Prize).
1st Prize + Rector’s Award
A two-vertex theorem for normal tilings
Krisztina Regős
supervisors: Gábor Domokos, Ákos G. Horváth
Normal tilings, consisting of mutually disjoint, non-overlapping cells of smooth, 2D manifolds may serve as models both for a broad variety of natural and also for man-made patterns [1]. Not only do they appear in several beautiful aspects of the nature (biology, geology and chemistry) but also, they provide the geometric description for a diversity of artificial objects. In architecture they not only may be used for the description of masonry structures or urban maps, but they can serve as mathematical models of mosaic pictures. Here we explore a curios metric property of such tessellations which appears to be particularly relevant from the point of view of applications: we prove that for periodic patterns the minimal average number of “sharp” vertices (i.e. vertices where adjacent edges are not at 180 degrees) is 2. We also give a general formula, expressing this minimal average value as a function of the Euler characteristic of the manifold and the number of edges of the tiling.
[1] B. Grünbaum and G.C. Shepard, Tilings and Patterns, Freeman and Co., New York, 1987.
1st Prize
Collision statistics in a hard sphere system
Anna Viczián
supervisors: János Török
Nowadays one of the most interesting problems in physics is predicting the behaviour of complex systems of particles, which exhibit a large variety of behaviours (eg. rainclouds, formation of solar systems, collective movement of animals, abrasion of pebbles, ect.), even though the interactions between particles are simple. Essentially all research in this area assumes that the particles are identical, this is because if their characteristics were to vary, predicting the evolution of the system would be much harder. Even those which assume only small irregularities are few and far between.
In this paper we study the relationship between the size of a particle and the number of times it collides in a heterogeneous hard sphere system, where only the size of particles varies. First we examine the system with an event driven simulation and find that the number of collisions as a function of the radius has a minimum. The rest of this paper is concerned with the mathematical description of this curve.
In our model we examine the number of times a particle (central sphere) collides from its frame of reference. We assume that other (free) spheres can come from any direction, but only a set distance derived from the spatial density of the particles. A free sphere can only collide with the central sphere if the angle of its velocity vector falls in a certain interval. Finally we get the number of collisions of the central sphere by taking the integral of all possible collision events weighted by the velocity. The curve we get by numerically solving this integral almost perfectly matches the curve given by the event driven simulation. This holds true for different size distributions.
3rd Prize + Csonka Pál Special Prize
Modelling abrasion of stone particles with iterated function systems – limits and potentials
Ágoston Szesztay
supervisors: Balázs Bárány, Gábor Domokos
This thesis presents the results since “Combinatoric and metric properties of polieders sliced on their edges” (BME, Építészmérnöki Kar, 2020) TDK thesis. In the previous thesis such polieders were examined, of which all vertices are chipped off by planes which can only intersect the edges starting from the vertex to be removed. Removed pyramids can not have common points. Resulting forms are simple polyhedra, their faces have 6 edges in average, the number of their faces and vertices are functions of the initial number of edges, the system of faces present self-similarity which is a common property of fractals. When cutting planes intersect edges according to proportion λ<1/2, the proportion of the limit area of the faces and the initial area can be determined, whereas starting from a regular polygon the limit of a face can only be circle if 2λ=1/(1+cos(ϕ) ).
The purpose of this thesis is the observation of fractal properties of polyhedra sliced on edges. The previous model is extended: edges starting from the vertex to be removed are cut according to λ_i and those points of the created edges which would be the part of the limit state divide the edge according to γ_i. Resulting geometry can be observed using iterated function systems (IFS). To illustrate the environs of one cubic vertex a Matlab code is presented using the identified IFS.
In general IFS only works is 3D. In some cases however - of which the conditions and an example is shown – the image of the 3D form projected to some planes can be drawn in 2D using IFS. Border curves of the faces can be differentiated only once to any combination of γ_i,λ_i. Higher differentiability is only possible if γ_i=λ_i=1/2.
It results in fractal properties combinatorically if cutting planes may cut down edges of the initial polyhedron. Modelling with IFS the geometry resulting from such events would be rather problematic.
Department’s Special Prize
Study of the stability of walls based on the force-indeterminacy
Kladuia Nagy
supervisors: János Török, Sára Lévay, Gábor Domokos
Walls represent an essential part of architectural creation. Stability and durability are crucial characteristics of walls. Builders have always tried to make enduring constructions therefore the geometry of walls has been optimized to reach the highest stability. Well known examples are brick walls, for which it is known for ca. ten thousand years, that they are the most stable when they are laid in perfect bond.
In my former TDK study titled “The geometry of walls” I have studied the vertex density of mosaics created from the surface pattern of walls. The vertex density ρ is introduced in the main field of convex mosaics of the walls. The main result of the former study is that based on only geometrical characterisation, vertex density can be a measure of stability in case of arbitrary wall structures.
However, this method cannot distinguish between cases where the vertex density remains the same, but the geometry varies. For example, all brick walls laid in bond have the vertex density of ρ=2,00 no matter of the offset (γ) of bricks even though the stability strongly depends on the offset between elements.
My goal is to define a clear measure describing the stability of walls. The main idea is that those structures where the standard deviation of contact forces acting between the bricks is small are the stable ones. Neither too small nor too large forces are ideal from the point of load bearing: in the former case the structure is not capable of having frictional forces, in the latter case the forces can result in overloading.
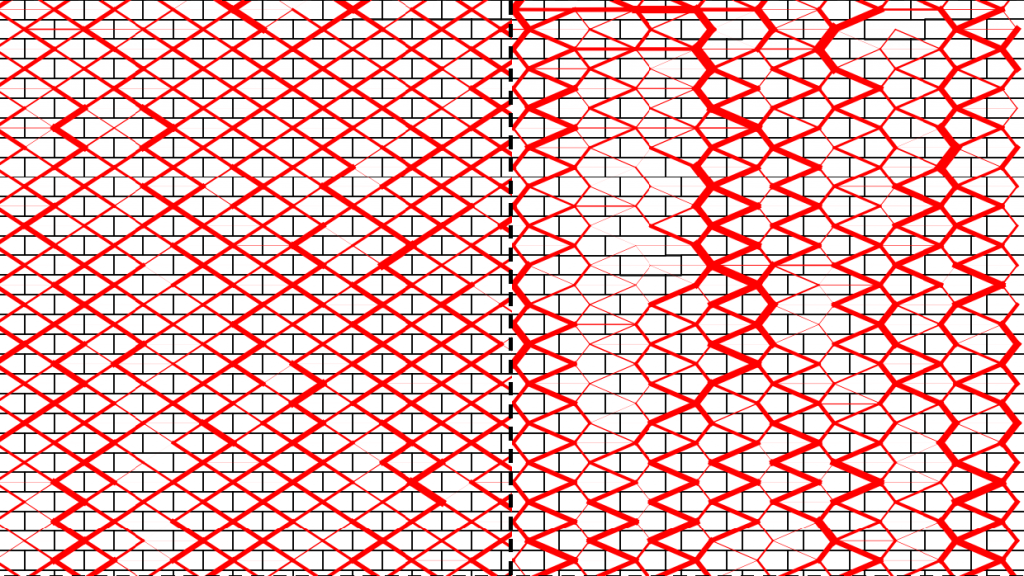
To verify my idea, I studied brick walls with contact dynamics simulations that define contact forces so that they satisfy the basic constraints (which are impenetrability and friction). Because the system is indeterminate, the algorithm – due to its stochastic nature – will provide a different random but stable force-network by every run. The earlier mentioned standard deviation of the forces can be computed based on these results.
To demonstrate the idea, I studied the best-known example: the brick wall. I have found that in case of γ=1/2 (left figure) the standard deviation of forces is small, the forces are similar, while in case of γ=1/4 (less stable configuration, right figure) the deviation is larger by 57%.
The presented method can be extended to arbitrary geometry, that makes the analysation of the stability of historical walls possible.
Metszet Journal Special Prize
Study of the stability of walls based on the force-indeterminacy
Máté Szondi
supervisors: András Árpád Sipos, Gábor Domokos
The shapes of pebbles provide a great deal of information about the natural erosion process, for example, sediment formation and the geophysical transport processes. For this reason, the topic is of great interest in contemporary geomorphology.
In geology, there are a few classification systems for the description of pebbles morphology. The oldest and most spread classification is the Zingg classification (1935)[1].
The Zingg classification approximates the shapes of the pebbles with an ellipsoid, the axis length of which is a≥b≥c, and it categorizes the shapes into four classes based on the axis ratios (y1,y2)=(c/a, b/a). For the Zingg classification, geologists measure the a>b>c axes and calculate the axes ratios. These measurements could include the data of several hundred thousand pieces of pebbles. For example, Carr measured 100,000 pebbles at Chesil Beach in the United Kingdom in 1969 [2][3]. In this study, I work with these axes ratios.
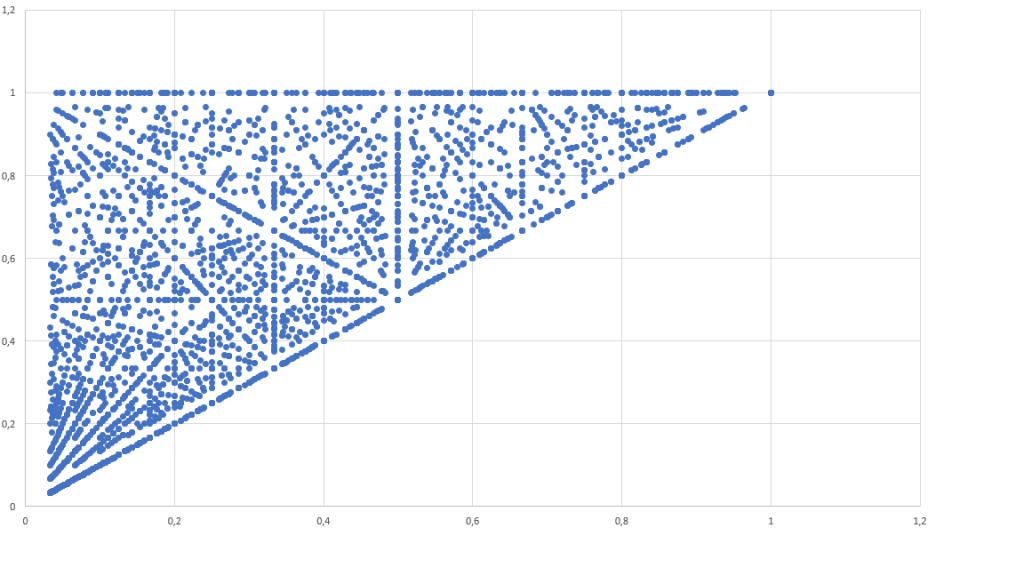
Since the measurement accuracy is finite, I assume that the a,b,c axis lengths are natural numbers. I approximate the field measurements with a random data set, so I assume that the a,b,c numbers are discreet, random variables with a uniform distribution in the [0,1…N], [0,1,…a],[0,1,…b] sets. I plot the axes ratios in a [y1,y2] coordinate system. It is expected that the distribution of the points is random. It is apparent that some of the points fit on lines in the data set. One might conclude that what should be random may not be random at all. In my study, I show that these lines appear naturally in the pattern. If these lines are not present, we can surmise that the data set is manipulated.
In my study, I define the visibility of the lines in the data set in the [y1,y2] space. Furthermore, I represent the slope of these lines via p/q relative primes. I put different numerosity data sets of points in Matlab and Excel. I conclude that the lower the norm of the multiplicative inverse of the vector (p,q) is, the more visible is the line.
Bibliography
[1] Zingg T.. 1935Beitrag zur Schotteranalyse. Mineral. Petrol. Mitte. 15, 39–140.
[2] Carr A. P.. 1969Size grading along a pebble beach: Chesil beach, England. J. Sedimentary Petrol. 39, 297–311.doi:10.1306/74D71C3A-2B21-11D7-8648000102C1865D (doi:10.1306/74D71C3A-2B21-11D7-8648000102C1865D).
[3] G. Domokos and G. W. Gibbons: 2012, The evolution of pebble size and shape in space and time, The Royal Society Publishing, https://doi.org/10.1098/rspa.2011.0562